Sách toán/Chuyển động

Chuyển động cong

Chuyển động cong v(t)

Chuyển Động v(t)		v	a	s
Cong		$v(t)$	$\frac{d}{dt}v(t)$	$\int v(t)dt$
Thẳng nghiêng		$at+v$	$a$	$\frac{1}{2}a{t}^2+vt+C$
Thẳng nghiêng		$at$	$a$	$\frac{a{t}^2}{2}+$
Thẳng ngang		$v$	$0$	$vt$
Thẳng dọc		$t$	$1$	$\frac{t^2}{2}$

Chuyển động cong s(t)

Chuyển Động s(t)		s	v	a
Cong		$s(t)$	$\frac{d}{dt}s(t)$	$\frac{d^2}{d{t}^2}s(t)$
Tròn		$r\theta (t)$	$r\frac{d}{dt}\theta (t)$	$r\frac{d^2}{d{t}^2}\theta (t)$

Dao động sóng

Dao động sóng sin

Dao động sóng sin ngang

$F_a=F_x$

$ma=-kx$

$\frac{d}{d{x}^2}x=-\frac{k}{m}x=-\beta x$

$x=Asin\omega t$

$\omega =\sqrt{\beta }$

Dao động sóng sin dọc

$F_a=F_y$

$ma=-ky$

$\frac{d}{d{x}^2}y=-\frac{k}{m}y=-\beta y$

$y=Asin\omega t$

$\omega =\sqrt{\beta }$

Dao động sóng sin nghiêng

$F_a=F_{\theta }$

$mg=-l\theta$

$\frac{d}{d{x}^2}\theta =-\frac{l}{m}\theta =-\beta \theta$

$\theta =Asin\omega t$

$\omega =\sqrt{\beta }$

Phương trình và hàm số sóng sin

Hàm số sóng sin có thể biểu diển bằng công thức toán của một Hàm số sóng lượng giác như sau

$f(t)=ASin(n\omega t)$

Mọi sóng sin đều thoả mãn một phương trình đạo hàm bậc n

$a{f}^n(t)+bf(t)=0$

Phương trình trên có thể viết dưới dạng phương trình sóng như sau

$f^n(t)=-\beta f(t)$

$\beta =\frac{b}{a}$

n ≥ 2

Chứng minh

Theo hoán chuyển Laplace

$F(s)=\int f(t)e^{-st}dt$

$f(t)$	$F(s)$
$\frac{d}{d{t}^n}$	$s^n$
$\frac{d}{d{t}^n}f(t)$	$s^{n}f(t)$

$a{f}^n(t)+bf(t)=0$

$s^{n}f(t)+\beta f(t)=0$

$s^n=-\beta =-\frac{b}{a}$

$s^n=\sqrt[n]{-\beta }=\pm j\sqrt[n]{\beta }=\pm jn\omega$

$f(t)=A{e}^{st}$

$f(t)=A{e}^{\pm jn\omega t}=Asin(n\omega t)$

$\omega =\sqrt[n]{\beta }$

n >= 2

Vector

Không gian 1 chiều

Đạo hàm bậc nhứt

Vector đường thẳng ngang

${\overrightarrow{X}}^{\text{'}}=\frac{d}{dt}\overrightarrow{X}=\frac{d}{dt}X\overrightarrow{i}=v_x\overrightarrow{i}$

Vector đường thẳng dọc

${\overrightarrow{Y}}^{\text{'}}=\frac{d}{dt}\overrightarrow{Y}=\frac{d}{dt}Y\overrightarrow{i}=v_y\overrightarrow{j}$

Vector đường thẳng nghiêng

${\overrightarrow{Z}}^{\text{'}}=\frac{d}{dt}\overrightarrow{Z}=\frac{d}{dt}Z\overrightarrow{i}=v_z\overrightarrow{k}$

Đạo hàm bậc hai

Vector đường thẳng ngang

${\overrightarrow{X}}^{{\text{'}}^{\prime }}=\frac{d^2}{d{t}^2}\overrightarrow{X}=\frac{d^2}{d{t}^2}X\overrightarrow{i}=a_x\overrightarrow{i}$

Vector đường thẳng dọc

${\overrightarrow{Y}}^{{\text{'}}^{\prime }}=\frac{d^2}{d{t}^2}\overrightarrow{Y}=\frac{d^2}{d{t}^2}Y\overrightarrow{i}=a_y\overrightarrow{j}$

Vector đường thẳng nghiêng

${\overrightarrow{Z}}^{{\text{'}}^{\prime }}=\frac{d^2}{d{t}^2}\overrightarrow{Z}=\frac{d^2}{d{t}^2}Z\overrightarrow{i}=a_z\overrightarrow{k}$

Không gian 2 chiều

Đạo hàm bậc nhứt

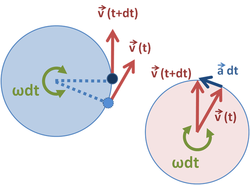
Vector đường tròn

${\overrightarrow{Z}}^{\text{'}}=(\overrightarrow{X}+\overrightarrow{Y}{)}^{\text{'}}=(\overrightarrow{X}{)}^{\text{'}}+(\overrightarrow{Y}{)}^{\text{'}}=(X\overrightarrow{i}{)}^{\text{'}}+(Y\overrightarrow{j}{)}^{\text{'}}=(R\overrightarrow{r}{)}^{\text{'}}$

${\overrightarrow{Z}}^{\text{'}}=\frac{d}{dt}(\overrightarrow{X}+\overrightarrow{Y})=\frac{d}{dt}(\overrightarrow{X})+\frac{d}{dt}(\overrightarrow{Y})=\frac{d}{dt}(X\overrightarrow{i})+\frac{d}{dt}(Y\overrightarrow{j})$

${\overrightarrow{Z}}^{\text{'}}=\frac{d}{dt}(R\overrightarrow{r})=R\frac{d}{dt}(\overrightarrow{r})+\overrightarrow{r}\frac{d}{dt}(R)=R\frac{d}{dt}(\overrightarrow{r})$