Sách công thức/Sách công thức giải tích

Hàm số

Tính chất

Hàm số	Công thức
Hàm số có dạng tổng quát	$f(x,y,z,...)$
Giá trị hàm số	$f(x,y,z,...)=C$

Loại hàm số

Dạng hàm số	Công thức	Thí dụ
Hàm số tuần hoàn Periodic function	$f(t)=f(t+T)$	$sinx=sin(x+k2\pi )$
Hàm số chẳn even function	$f(x)=f(-x)$	$y(x)=|x|$
Hàm số lẽ odd function	$f(x)=-f(x)$	$y(x)=-y(x)$
Hàm số nghịch đảo inverse function	$f^{-1}(x)=\frac{1}{f(x)}$	$si{n}^{-1}x=\frac{1}{sinx}$
Hàm số trong hàm số composite function	$f(x)=f(g(x))$
Hàm số nhiều biến số parametric function	$z=f(x,y)$
Hàm số tương quan/]] recursive function

Phép toán hàm số

Đồ thị hàm số

Với mọi giá trị của x sẻ có một giá trị hàm số của x tương đương . Thí dụ, với hàm số f(x)=x ta có thể thiết lập bảng giá trị tương quan của x và hàm số của x . Khi đặt các giá trị của x và của f(x) trên đồ thị XY ta có thể vẻ được hình đường thẳng có độ góc bằng 1 đi qua điểm gốc ở tọa độ (0,0)

x	-2	-1	0	1	2	Hình
F(x)=x	-2	-1	0	1	2

Đồ thị hàm số	Thẳng	Cong	Tròn	Lũy thừa	Log	Lượng giác
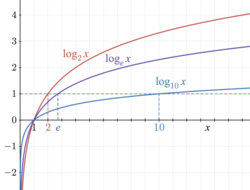
	Đồ thị Hàm số đường thẳng	Đồ thị Hàm số đường cong	Đồ thị Hàm số vòng tròn	Đồ thị Hàm số lũy thừa	Đồ thị hàm số Log	Đồ thị hàm số lượng giác $\cos x$ $\sin x$ $\tan x$ $\cot x$ $\sec x$ $\csc x$

x

Công thức toán

Danh sách các hàm số	Ý nghỉa	Công thức
Hàm số đường thẳng	Hàm số đường thẳng qua 2 điểm bất kỳ	$Y=ZX$ $y=y_o+Z(x-x_o)$
Hàm số vòng tròn Z đơn vị		$Z^2=X^2+Y^2$
Hàm số vòng tròn 1 đơn vị		${\frac{Z}{Z}}^2={\frac{X}{Z}}^2+{\frac{Y}{Z}}^2$ $1=co{s}^2+si{n}^2$ v $1=se{c}^2+ta{n}^2$ $1=cs{c}^2+co{t}^2$|-
Hàm số lượng giác		$cos\theta =\frac{X}{Z}$ $sin\theta =\frac{Y}{Z}$ $sec\theta =\frac{1}{X}$ $csc\theta =\frac{1}{Y}$ $tan\theta =\frac{Y}{X}$ $cot\theta =\frac{X}{Y}$
Hàm số lũy thừa Power function		$y=a{x}^n$
Hàm số Lô ga rít		$y(x)=Logx$
Hàm số tổng lũy thừa n degree Polynomial function		$y(x)=a{x}^n+a_{n-1}{x}^{n-1}+...+a_0{x}^0$
Hàm số chia/]] Rational function		$Q(x)=\frac{N(x)}{M(x)}-R(x)$

Biểu diển hàm số bằng tổng dải số Maclaurin

Dải số Maclaurin

Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau $f(x)=a_0+a_{1}x+a_2{x}^3+a_4{x}^4+...=f(0)+f^{\text{'}}x(0)+\frac{f^{{\text{'}}^{\prime }}(0)}{2!}+\frac{f^{{\text{'}}^{″}}(0)}{3!}+...$

Chứng minh

Khi x=0 $f(0)=a_0$ Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0 $f^{\text{'}}(x)=a_1+2a_{2}x+3a_3{x}^2+4a_4{x}^3$ $f^{\text{'}}(0)=a_1$ Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0 $f^{{\text{'}}^{\prime }}(x)=2a_2+(3)(2)a_{3}x+(4)(3)a_4{x}^2+(5)(4)a_5{x}^3$ $f^{{\text{'}}^{\prime }}(0)=2a_2$ $a_2=\frac{f^{{\text{'}}^{\prime }}(0)}{2}$ Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0 $f^{{\text{'}}^{″}}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_5{x}^2$ $f^{{\text{'}}^{″}}(0)=(3)(2)a_3$ $a_3=\frac{f^{{\text{'}}^{″}}(0)}{3!}$ Thế $a_0,a-1,a-2$ vào hàm số ở trên $f(x)=a_0+a_{1}x+a_2{x}^3+a_4{x}^4$ ta được $f(x)=f(0)+f^{\text{'}}x(0)+\frac{f^{{\text{'}}^{\prime }}(0)}{2!}+\frac{f^{{\text{'}}^{″}}(0)}{3!}$

Toán giải tích

Biến đổi hàm số		$a=\frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}=\frac{f(x+\mathrm{\Delta }x)-f(x)}{(x+\mathrm{\Delta }x)-x}=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{y-y_o}{x-x_o}$
Đạo hàm hàm số		$\frac{d}{dx}f(x)=f^{\text{'}}(x)=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum \frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum \frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$
Tích phân xác định		$\underset{a}{\overset{b}{\int }}f(x)dx=F(b)-F(a)$
Tích phân bất định		$\int f(x)dx=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum (f(x)+\frac{\mathrm{\Delta }f(x)}{2})\mathrm{\Delta }x=F(x)+C$

Phương trình

Dạng tổng quát

Phương trình có dạng tổng quát

$f(x,y,z,...)=0$

Loại phương trình

Phương trình lũy thừa	Dạng tổng quát
Phương trình lũy thừa bậc 1	$ax+b=0$
Giải phương trình lũy thừa bậc 2	$a{x}^2+bx+c=0$
Giải phương trình lũy thừa bậc n	$a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_o=0$

Giải phương trình

Giải phương trình lũy thừa

Phương trình lũy thừa	Dạng tổng quát	Giải phương trình
Phương trình lũy thừa bậc 1	$ax+b=0$	$x+\frac{b}{a}=0$ $x=-\frac{b}{a}$
Giải phương trình lũy thừa bậc 2	$a{x}^2+bx+c=0$	$x^2+\frac{b}{a}x+\frac{c}{a}=0$ :$x^2+\frac{b}{a}x=-\frac{c}{a}.$ $x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=-\frac{c}{a}+\frac{b^2}{4a^2}$. ${(x+\frac{b}{2a})}^2=\frac{b^2-4ac}{4a^2}$. $x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}$. $x=\frac{-b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$ $x=\frac{-b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$ $a{x}^n+b=0$ $a{x}^n=-b$ v$x^n=-\frac{b}{a}$ $x=n\sqrt{-\frac{b}{a}}=\pm jn\sqrt{\frac{b}{a}}$ $x=n\sqrt{-\frac{b}{a}}=\pm jn\sqrt{\frac{b}{a}}$
Giải phương trình lũy thừa bậc n	$a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_o=0$

Giải phương trình đạo hàm

Phương trình đạo hàm	Dạng tổng quát	Giải phương trình
Phương trình đạo hàm bậc n	$a\frac{d^n}{d{x}^n}f(x)+bf(x)=0$	$s^{n}f(x)+\frac{b}{a}f(x)=0$ $s^n=-\frac{b}{a}$ $s=n\sqrt{-\frac{b}{a}}=\pm jn\sqrt{\frac{b}{a}}=\pm j\omega$ $f(x)=A{e}^{st}=A{e}^{\pm j\omega t}=Asin\omega t$ . Với $n$ ≥ 2
Phương trình đạo hàm bậc 2	$a\frac{d^2}{d{x}^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0$	$s^{2}f(x)+\frac{b}{a}sf(x)+\frac{c}{a}f(x)=0$ $s^2+2\alpha s+\beta =0$ $s=-\alpha$ . $f(x)=A{e}^{-\alpha x}=A(\alpha )$ . $\alpha$ = $\beta$ $s=-\alpha \pm \lambda$ . $f(x)=A{e}^{(-\alpha \pm \lambda )x}=A(\alpha )e^{\lambda x}+A(\alpha )e^{-\lambda x}$ . $\alpha$ < $\beta$ $s=-\alpha \pm j\omega$ . $f(x)=A{e}^{(-\alpha \pm j\omega )x}=A(\alpha )sin\omega$ . $\alpha$ > $\beta$ $\alpha =\frac{b}{2a}$ . $\beta =\frac{c}{a}$ . $\lambda =\sqrt{\alpha -\beta }$ . $\omega =\sqrt{\beta -\alpha }$
Phương trình đạo hàm bậc 1	$a\frac{d}{dx}f(x)+bf(x)=0$	$sf(x)+\frac{b}{a}f(x)=0$ $s=-\frac{b}{a}$ $f(x)=A{e}^{sx}=A{e}^{-\frac{b}{a}x}=A{e}^{-\alpha x}$