Sách toán kỹ sư
Ký số
Loại Ký số Biểu tượng số Ký số La Mã I II III IV V VI VII VIII IX X Ký số Ả rập 1 2 3 4 5 6 7 8 9 10 Ký số Trung quốc - = Giá trị 1 2 3 4 5 6 7 8 9 10
Số đại số
Toán đại số dùng chữ cái a-z, A-Z đại diện cho các con số số học từ 0 đến 9. Thí dụ như A = 3 , B = 2 . Các chữ cái đại diện cho các con số số học được gọi là Biến số.
Loai số đại số và Phép toán đại số
Số đại số được phân loai thành các loại số dưới đây
Loai số đại số Định nghỉa Ký hiệu Thí dụ Số tự nhiên /Số chẳn/ Mọi số tự nhiên chia hết cho 2 Số lẻ Mọi số tự nhiên không chia hết cho 2 Số nguyên tố Mọi số tự nhiên chia hết cho 1 và cho chính nó /Số nguyên/ /Phân số/ /Số phức/
Phép toán đại số
Các phép toán thực thi trên các số đại số bao gồm
Toán Ký Hiệu Công Thức Định Nghỉa /Toán cộng/ Toán Cộng hai số đại số /Toán trừ/ Toán Trừ hai số đại số /Toán nhân/ Toán Nhân hai số đại số /Toán chia/ Toán Chia hai số đại số /Toán lũy thừa/ Toán tìm tích n lần của chính số nhân /Toán căn/ nếu có Toán lủy thừa nghịch
Số tự nhiên
Số nguyên
Loai số Số nguyên
Số nguyên là số đại số bao gồm ba loại số số nguyên âm , số nguyên dương và số không . Số không có giá trị bằng 0 . Số nguyên âm có giá trị nhỏ hơn 0 . Số nguyên dương có giá trị lớn hơn 0 . Thí dụ như -1,0,+1 .
Số nguyên có ký hiệu chung . Số nguyên âm có ký hiệu chung . Số nguyên dươngcó ký hiệu chung .: Số không . Thí dụ Số nguyên trong tập hợp số tự nhiên từ 0 đến 9 . Số nguyên âm . . Số nguyên dương . . Số nguyên không .
Phép toán Số nguyên
Số nguyên
Toán Số nguyên Công thức Cộng trừ nhân chia số nguyên với số không
Cộng trừ nhân chia số nguyên dương với số nguyên âm
Cộng trừ nhân chia số nguyên dương với số nguyên dương
Lũy thừa số nguyên
. . VớiCăn số nguyên
Phân số
Số Phức là số có dạng tổng quát
Số thập phân
Số hửu tỉ
Số vô tỉ
Số Phức
Số Phức là số có dạng tổng quát
Phép toán số đại số
Phép toán Số nguyên
Số nguyên
Toán Số nguyên Công thức Cộng trừ nhân chia số nguyên với số không
Cộng trừ nhân chia số nguyên dương với số nguyên âm
Cộng trừ nhân chia số nguyên dương với số nguyên dương
Lũy thừa số nguyên
. . VớiCăn số nguyên
Phép toán Phân số
Đổi hổn số thành phân số
Cộng , Trừ, Nhân, Chia 2 phân số
Lũy thừa phân số
Căn phân số
Phép toán Toán số phức
Số phức được biểu diển như ở dưới đây
Số phức Thuận Nghịch Biểu diển dưới dạng xy Biểu diển dưới dạng Zθ Biểu diển dưới dạng hàm số lượng giác Biểu diển dưới lũy thừa của e
Toán số phức được thực thi như sau
Toán Số phức Toán cộng Toán trừ Toán nhân Toán chia và và và và
Định lý Demoive
Phép toán Lũy thừa
| Toán lủy thừa | Công thức |
| Lủy thừa không | |
| Lủy thừa 1 | |
| Lủy thừa của số không | |
| Lủy thừa của số 1 | |
| Lủy thừa trừ | |
| Lủy thừa phân số | |
| Lủy thừa của số nguyên âm |
|
| Lủy thừa của số nguyên dương | |
| Lủy thừa của lủy thừa | |
| Lủy thừa của tích hai số | |
| Lủy thừa của thương hai số | |
| Lủy thừa của căn | |
| Cộng trừ nhân chia 2 lủy thừa |
|
Lủy thừa của tổng hai số |
|
| Lủy thừa của hiệu hai số |
|
| Hiệu 2 lũy thừa | |
| Tổng 2 lũy thừa |
Phép toán Toán căn
- khi có
Toán căn số Công thức Căn và lủy thừa Căn của số nguyên
Căn lủy thừa
Căn thương số
Căn tích số
=Vô căn
Ra căn
Phép toán Toán log
- khi có
Toán Log Công thức Viết tắc
Log 1
Log lũy thừa
Lũy thừa log
Log của tích số
Log của thương số
Log của lủy thừa
Đổi nền log
Dải số đại số
Dải số
Dải Số là một chuổi số có định dạng . Thí dụ
Dải số của các số tự nhiên Dải số của các số tự nhiên chẳn Dải số của các số tự nhiên lẻ
Tổng dải số đại số
Chuổi sô Định nghỉa Ký hiệu Thí dụ Chuổi số phép toán tìm tổng của một dải số
Tổng chuổi số cấp số cộng
Dạng tổng quát
Chứng minh
Thí dụ
Dải số cấp số cộng có dạng tổng quát
Tổng số của dải số
Cách giải
Tổng chuổi số cấp số nhân
Dạng tổng quát
Chứng minh
-
- với
Thí dụ
Tổng chuổi số Pascal
Công thức tổng quát lũy thừa n của một tổng
Với
Thí dụ
Từ trên , ta thấy hằng số trước biến số x tạo hình tam giác Pascal dưới đây
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
Tổng chuổi số Taylor
Dạng tổng quát
Tổng dải số Fourier

Tổng chuổi số Fourier đại diện cho tổng chuổi số hàm số sóng sine
Công thức tổng dải số
- where is some constant.
Biểu thức đại số
Biểu thức Đơn thức Đa thức Đẳng thức Bất đẳng thức , , , > , <
Hằng đẳng thức
Hằng đẳng thức Công thức Bình phương tổng 2 số đại số Bình phương hiệu 2 số đại số Tổng 2 bình phương
Hiệu 2 bình phương Tổng 2 lập phương Hiệu 2 lập phương
Bất đẳng thức
Hàm số đại số
Tính chất
Hàm số Công thức Hàm số có dạng tổng quát Giá trị hàm số
Loại hàm số
Dạng hàm số Công thức Thí dụ Hàm số tuần hoàn Periodic function Hàm số chẳn even function Hàm số lẽ odd function Hàm số nghịch đảo inverse function Hàm số trong hàm số composite function Hàm số nhiều biến số parametric function Hàm số tương quan/]] recursive function
Phép toán hàm số
Đồ thị hàm số
Với mọi giá trị của x sẻ có một giá trị hàm số của x tương đương . Thí dụ, với hàm số f(x)=x ta có thể thiết lập bảng giá trị tương quan của x và hàm số của x . Khi đặt các giá trị của x và của f(x) trên đồ thị XY ta có thể vẻ được hình đường thẳng có độ góc bằng 1 đi qua điểm gốc ở tọa độ (0,0)
Công thức toán
Danh sách các hàm số Công thức Hàm số đường thẳng
Hàm số vòng tròn Z đơn vị
Hàm số vòng tròn 1 đơn vị
Hàm số lượng giác
Hàm số lũy thừa Power function
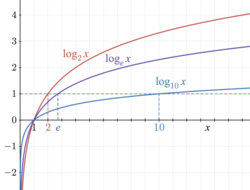
Hàm số Lô ga rít
Hàm số tổng lũy thừa n degree Polynomial function
Hàm số chia/]] Rational function
Biểu diển hàm số bằng tổng dải số Maclaurin
Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau
Chứng minh
Khi x=0
Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0
Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0
Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0
Thế vào hàm số ở trên ta được
Toán giải tích - Phép toán hàm số
Với đường thẳng nghiêng đi qua 2 điểm (xo,yo) - (x,y) dưới đây
Ta có thể tính các loại toán sau
- Biến đổi hàm số
Biến đổi hàm số cho biết tỉ lệ thay đổi biến số y trên thay đổi biến số x có thể biểu diển bằng công thức toán dưới đây
Với
- - Thay đổi biến số x
- - Thay đổi biến số y
- Diện tích dưới hình
Với mọi đường cong bên dưới
Ta có thể tính các loại toán sau
- Tích phân xác định đường cong
- Tích phân bất định đường cong
Phương trình đại số
Dạng tổng quát
Phương trình có dạng tổng quát
Giải phương trình
Quá trình tìm giá trị nghiệm số thỏa mản
Giải phương trình lũy thừa
Phương trình lũy thừa Dạng tổng quát Giải phương trình Phương trình lũy thừa bậc 1
Giải phương trình lũy thừa bậc 2
:
.
.
.
v
Giải phương trình lũy thừa bậc n
Giải phương trình đạo hàm
Phương trình đạo hàm Dạng tổng quát Giải phương trình Phương trình đạo hàm bậc n Phương trình đạo hàm bậc 2
. . =
. . <
. . >
. . .Phương trình đạo hàm bậc 1
Giải hệ phương trình tuyến tính
Dạng tổng quát của 2 biến số
Hình học Eucleur
Điểm
Góc Định nghỉa Ký hiệu Đơn vị Thí dụ . Một chấm A __ B
Đường thẳng
Góc
Góc Định nghỉa Ký hiệu Đơn vị Thí dụ 
Khi hai đường thẳng cắt nhau tại một điểm
sẽ tạo ra một góc giữa hai đường thẳng
Đường thẳng
Định nghỉa
Tọa độ điểm đại số
Đường thẳng là một đường nối liền giửa 2 điểm (xo,yo) - (x,y)
Có độ dóc tính bằng
Có thể biểu diển bằng hàm số toán đại số dưới đây
Dạng đường thẳng
Đường thẳng vuông góc
Khi hai đường thẳng cắt nhau tại một điểm tạo nên một góc vuông 90o sẻ tạo ra hai Đường thẳng vuông góc voi nhau
Đường thẳng AB vuông góc với đường thẳng CD
- Góc B đỏ = Góc B xanh = 90o
Góc B đỏ + Góc B xanh = 90o + 90o = 180o
Góc B đỏ = 180o - Góc B xanh
Góc B xanh = 180o - Góc B đỏ
Đường thẳng song song
Hai đường thẳng không cắt nhau tại bất kỳ điểm nào là đường thẳng song song . Hai đường thẳng song song là hai đường thẳng không có điểm chung . Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song . Ký hiệu đường thẳng song song
- AB // CD
Tính chất góc trong 2 đương thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
- Hai góc so le trong bằng nhau;
- Hai góc đồng vị bằng nhau;
- Hai góc trong cùng phía bù nhau.
Vector đường thẳng
Vector đường thẳng là một đường thẳng có hướng và có một độ dài . Vectơ đường thẳng có ký hiệu Vector → . Thí dụ, Vector
Mọi vector A đều có thể biểu diển bằng cường độ vector nhân với vector đơn vị như dưới đây
Với
- - Vector
- . Cường độ vector
- . Vector 1 đơn vị
Cường độ vector
Vector 1 đơn vị
Thí dụ
Tam giác vuông Pythagore
Vector đương thẳng Công tức toán Vector đương thẳng ngang Vector đương thẳng dọc Vector đương thẳng nghiêng
Vòng tròn Eucleur
Vector bán kín vòng tròn
Phép toán vector
Không gian 2 chiều
Cộng vector

Phép cộng hai vectơ: tổng của hai vectơ và là một vectơ được xác định theo quy tắc:
- Quy tắc 3 điểm
- di chuyển vectơ sao cho điểm đầu C của trùng với điểm cuối B của : . Khi đó vectơ có điểm gốc đặt tại điểm A, điểm cuối đặt tại D, chiều từ A đến D là vectơ tổng
- Quy tắc hình bình hành
- di chuyển vectơ đến vị trí trùng điểm gốc A của vectơ . Khi đó vectơ tổng có gốc đặt tại điểm A, có điểm cuối đặt tại góc đối diện trong hình bình hành tạo ra bởi hai vectơ thành phần và , chiều từ gốc A đến điểm cuối
Tính chất Vectơ Công thức Tính chất giao hoán Tính chất kết hợp Tính chất của vectơ-không Với 3 điểm A, B, C thẳng hàng ta có: I là trung điểm đoạn thẳng AB G là trọng tâm
Trừ vector
Nhân vector
Với hai vectơ bất kì, với hằng số h và k, ta có
Không gian 3 chiều
Chấm 2 vector
Tích vô hướng của hai vectơ A = [A1, A2,..., An] và B = [B1, B2,..., Bn] được định nghĩa như sau
- . Trong đó θ là góc giữa A và B.
Trường hợp đặc biệt,
- Nếu A và B trực giao thì góc giữa chúng là 90°, do đó:
- Nếu chúng cùng hướng thì góc giữa chúng là 0°, do đó:
Suy ra tích vô hướng của vectơ A và chính nó là:
ta có:
là khoảng cách Euclid của vectơ, luôn có giá trị dương khi A khác 0.
Cho vectơ A = [A1, A2,..., An] ta có
Cho a, b, và c là các vectơ và r là đại lượng vô hướng, tích vô hướng thỏa mãn các tính chất sau:.
- Giao hoán:
- được suy ra từ định nghĩa (θ góc giữa a và b):
- Phân phối cho phép cộng vectơ:
- Dạng song tuyến:
- Phép nhân vô hướng:
- Không có tính kết hợp bởi vì tích vô hướng giữa đại lượng vô hướng (a ⋅ b) và vectơ (c) không tồn tại, tức là biểu thức cho tính kết hợp: (a ⋅ b) ⋅ c or a ⋅ (b ⋅ c) là không hợp lệ.
- Trực giao:
- Hai vectơ khác vectơ không: a và b trực giao khi và chỉ khi a ⋅ b = 0.
- Hai vectơ trực giao trong không gian Euclid còn được gọi là vuông góc.
- Không có tính khử:
- Tính khử cho phép nhân của các số được định nghĩa như sau: nếu
- ab = ac, thì b luôn luôn bằng c nếu a khác 0. Tích vô hướng không tuân theo tính khử:
- Nếu a ⋅ b = a ⋅ c và a ≠ 0, thì ta có: a ⋅ (b − c) = 0 theo như luật phân phối; suy ra a trực giao với (b − c), tức là (b − c) ≠ 0, và dẫn đến b ≠ c.
- Quy tắc đạo hàm tích: Nếu a và b là hàm số, thì đạo hàm của a ⋅ b là a′ ⋅ b + a ⋅ b′.

Hai vectơ a và b có góc giữa hai vectơ là θ (như trong hình bên phải) tạo thành một tam giác có cạnh thứ ba là c = a − b. Tích vô hướng của c và chính nó là Định lý cos:
Chéo 2 vector


Phép nhân vectơ của vectơ a và b được ký hiệu là a × b hay , định nghĩa bởi:
với θ là góc giữa a và b (0° ≤ θ ≤ 180°) nằm trên mặt phẳng chứa a và b, và n là vectơ đơn vị vuông góc với a và b.
Thực tế có hai vectơ n thỏa mãn điều kiện vuông góc với a và b (khi a và b không cùng phương), vì nếu n vuông góc với a và b thì -n cũng vậy.
Việc chọn hướng của véctơ n phụ thuộc vào hệ tọa độ tuân theo quy tắc bàn tay trái hay quy tắc bàn tay phải. (a, b, a × b) tuân cùng quy tắc với hệ tọa độ đang sử dụng để xác định các vectơ.
Vì kết quả phụ thuộc vào quy ước hệ tọa độ, nó được gọi là giả vectơ. May mắn là trong các hiện tượng tự nhiên, nhân vectơ luôn đi theo cặp đối chiều nhau, nên kết quả cuối cùng không phụ thuộc lựa chọn hệ tọa độ.
Trong không gian với hệ trục tọa độ Oxyz, cho và , khi đó tích có hướng giữa 2 vectơ là vectơ có tọa độ
Ứng dụng
Nhiều công thức tính trong không gian vectơ ba chiều liên quan đến nhân vectơ, nhờ vào kết quả là vectơ vuông góc với hai vectơ đầu vào.
- Diện tích hình bình hành ABCD:
- Thể tích khối hộp ABCDA'B'C'D':
- 2 vector và cùng phương
- 3 vector , , đồng phẳng
Góc
Định nghỉa
Góc Định nghỉa Ký hiệu Đơn vị Thí dụ 
Khi hai đường thẳng cắt nhau tại một điểm
sẽ tạo ra một góc giữa hai đường thẳng
Thể loại góc
Hình tam giác

- 3 điểm .
- 3 cạnh .
- 3 góc .
Chu vi Diện tích Thể tích
Chu vi Diện tích Thể tích
Tam giác thường
Định lý Sin
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng
- .
trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:
Định lý Cosin
Tam giác vuông
Tam giác vuông là một loại tam giác có 2 cạnh vuông góc với nhau cắt nhau tại một điểm tạo nên một góc vuông bằng

- c - Cạnh huyền
- a - Cạnh đối
- b - Cạnh kề
- Tam giác có 2 cạnh vuông góc với nhau tạo ra một góc vuông 90o
Định lý tam giác vuông
- Tam giác có 1 góc vuông là tam giác vuông
- Tam giác có 2 góc nhọn phụ nhau là tam giác vuông
- Tam giác có bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh kia là tam giác vuông (định lý Pytago đảo)
- Tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy là tam giác vuông
- Tam giác nội tiếp đường tròn có 1 cạnh là đường kính thì tam giác đó vuông
- Tam giác có cạnh đối diện góc 30° bằng một nửa một cạnh khác trong tam giác thì tam giác đó vuông.
Định lý Pytago
Định lý Pytago phát biểu rằng:
- Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này . Nó được thể hiện bằng phương trình
Trong đó, c là chiều dài của cạnh huyền và a và b là chiều dài của hai cạnh còn lại.
Hàm số lượng giác
Tương quan các cạnh và góc
Tam giác vuông trên đồ thị XY
Hàm số cạnh Độ dài cạnh ngang
Độ dài cạnh dọc Độ dóc Độ nghiêng
Vector đương thẳng ngang
Vector đương thẳng dọc Vector đương thẳng nghiêng
Hàm số Đường thẳng nghiêng ở độ dóc Z
Hàm số Đường thẳng nghiêng ở độ góc nghiêng θ
Diện tích dưới hình
Hình cong
Độ nghiêng đường thẳng
Diện tích dưới hình
Khi
Độ nghiêng đường thẳng
Diện tích dưới hình
Diện tích dưới hình giửa 2 điểm
Hàm số lượng giác cơ bản
Định nghỉa
6 Công thức hàm số lượng giác cơ bản định nghỉa tương quan giửa các cạnh và góc trong tam giác vuông
Tính chất
Tuần hoàn
Đối xứng
Tịnh tiến
Đẳng thức sau cũng đôi khi hữu ích:
với
Góc bội
Nếu Tn là đa thức Chebyshev bậc n thì
công thức de Moivre:
Hàm hạt nhân Dirichlet Dn(x) sẽ xuất hiện trong các công thức sau:
Hay theo công thức hồi quy:
- =
Góc chia đôi
Từ trên , Nhân với mẫu số và tử số 1 + cos x, rồi dùng định lý Pytago để đơn giản hóa:
Tương tự, lại nhân với mẫu số và tử số của phương trình (1) bởi 1 − cos x, rồi đơn giản hóa:
Suy ra:
Nếu
thì:
| and | and |
Tổng 2 góc
Hiệu 2 góc
Tích 2 góc
Lũy thừa góc
Hàm số lượng giác nghịch
Hàm số lượng đường thẳng
Hàm số lượng đường thẳng nghiêng
Hàm số lượng đường thẳng dọc
Hàm số lượng đường thẳng ngang
Hàm số lượng đường tròn
Hàm số lượng đường tròn Z đơn vị
Hàm số lượng đường tròn 1 đơn vị
Vector
Vector đại diện cho một đường thẳng có hướng và có một độ dài . Vectơ có ký hiệu → . Thí dụ, Vector
Tính chất
Mọi vector A đều có thể biểu diển bằng cường độ vector nhân với vector đơn vị như dưới đây
Với
- - Vector
- . Cường độ vector
- . Vector 1 đơn vị
Cường độ vector
Vector 1 đơn vị
Thí dụ
Trong hệ tọa độ XY
Vector chuyển động thẳng hàng ngang Vector chuyển động thẳng hàng dọc Vector chuyển động thẳng hàng nghiêng Vector chuyển động tròn
Chuyển Động s v a Cong 
Vector đương thẳng ngang
→→
Vector đương thẳng dọc
↑
↑
Vector đương thẳng nghiêng
Vector đương tròn
Vector đương tròn
Operator notation
Gradient
For a function in three-dimensional Cartesian coordinate variables, the gradient is the vector field:
where i, j, k are the standard unit vectors for the x, y, z-axes. More generally, for a function of n variables , also called a scalar field, the gradient is the vector field: where are mutually orthogonal unit vectors.
As the name implies, the gradient is proportional to, and points in the direction of, the function's most rapid (positive) change.
For a vector field , also called a tensor field of order 1, the gradient or total derivative is the n × n Jacobian matrix:
For a tensor field of any order k, the gradient is a tensor field of order k + 1.
For a tensor field of order k > 0, the tensor field of order k + 1 is defined by the recursive relation where is an arbitrary constant vector.
Divergence
In Cartesian coordinates, the divergence of a continuously differentiable vector field is the scalar-valued function:
As the name implies, the divergence is a (local) measure of the degree to which vectors in the field diverge.
The divergence of a tensor field of non-zero order k is written as , a contraction of a tensor field of order k − 1. Specifically, the divergence of a vector is a scalar. The divergence of a higher-order tensor field may be found by decomposing the tensor field into a sum of outer products and using the identity, where is the directional derivative in the direction of multiplied by its magnitude. Specifically, for the outer product of two vectors,
For a tensor field of order k > 1, the tensor field of order k − 1 is defined by the recursive relation where is an arbitrary constant vector.
Curl
In Cartesian coordinates, for the curl is the vector field: where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively.
As the name implies the curl is a measure of how much nearby vectors tend in a circular direction.
In Einstein notation, the vector field has curl given by: where = ±1 or 0 is the Levi-Civita parity symbol.
For a tensor field of order k > 1, the tensor field of order k is defined by the recursive relation where is an arbitrary constant vector.
A tensor field of order greater than one may be decomposed into a sum of outer products, and then the following identity may be used: Specifically, for the outer product of two vectors,
Laplacian
In Cartesian coordinates, the Laplacian of a function is
The Laplacian is a measure of how much a function is changing over a small sphere centered at the point.
When the Laplacian is equal to 0, the function is called a harmonic function. That is,
For a tensor field, , the Laplacian is generally written as: and is a tensor field of the same order.
For a tensor field of order k > 0, the tensor field of order k is defined by the recursive relation where is an arbitrary constant vector.
Special notations
In Feynman subscript notation, where the notation ∇B means the subscripted gradient operates on only the factor B.[1][2]
Less general but similar is the Hestenes overdot notation in geometric algebra.[3] The above identity is then expressed as: where overdots define the scope of the vector derivative. The dotted vector, in this case B, is differentiated, while the (undotted) A is held constant.
For the remainder of this article, Feynman subscript notation will be used where appropriate.
First derivative identities
For scalar fields , and vector fields , , we have the following derivative identities.
Distributive properties
First derivative associative properties
Product rule for multiplication by a scalar
We have the following generalizations of the product rule in single-variable calculus.
Quotient rule for division by a scalar
Chain rule
Let be a one-variable function from scalars to scalars, a parametrized curve, a function from vectors to scalars, and a vector field. We have the following special cases of the multi-variable chain rule.
For a vector transformation we have:
Here we take the trace of the dot product of two second-order tensors, which corresponds to the product of their matrices.
Dot product rule
where denotes the Jacobian matrix of the vector field .
Alternatively, using Feynman subscript notation,
See these notes.[4]
As a special case, when Bản mẫu:Math,
The generalization of the dot product formula to Riemannian manifolds is a defining property of a Riemannian connection, which differentiates a vector field to give a vector-valued 1-form.
Cross product rule
Note that the matrix is antisymmetric.
Second derivative identities
Divergence of curl is zero
The divergence of the curl of any continuously twice-differentiable vector field A is always zero:
This is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.
Divergence of gradient is Laplacian
The Laplacian of a scalar field is the divergence of its gradient: The result is a scalar quantity.
Divergence of divergence is not defined
The divergence of a vector field A is a scalar, and the divergence of a scalar quantity is undefined. Therefore,
Curl of gradient is zero
The curl of the gradient of any continuously twice-differentiable scalar field (i.e., differentiability class ) is always the zero vector:
It can be easily proved by expressing in a Cartesian coordinate system with Schwarz's theorem (also called Clairaut's theorem on equality of mixed partials). This result is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.
Curl of curl
Here ∇2 is the vector Laplacian operating on the vector field A.
Curl of divergence is not defined
The divergence of a vector field A is a scalar, and the curl of a scalar quantity is undefined. Therefore,
Second derivative associative properties

A mnemonic
The figure to the right is a mnemonic for some of these identities. The abbreviations used are:
- D: divergence,
- C: curl,
- G: gradient,
- L: Laplacian,
- CC: curl of curl.
Each arrow is labeled with the result of an identity, specifically, the result of applying the operator at the arrow's tail to the operator at its head. The blue circle in the middle means curl of curl exists, whereas the other two red circles (dashed) mean that DD and GG do not exist.
Summary of important identities
Differentiation
Gradient
Divergence
Curl
Vector-dot-Del Operator
Second derivatives
Third derivatives
Integration
Below, the curly symbol ∂ means "boundary of" a surface or solid.
Surface–volume integrals
In the following surface–volume integral theorems, V denotes a three-dimensional volume with a corresponding two-dimensional boundary S = ∂V (a closed surface):
- Bản mẫu:Oiint
- Bản mẫu:Oiint (divergence theorem)
- Bản mẫu:Oiint
- Bản mẫu:Oiint (Green's first identity)
- Bản mẫu:Oiint (Green's second identity)
- Bản mẫu:Oiint (integration by parts)
- Bản mẫu:Oiint (integration by parts)
- Bản mẫu:Oiint (integration by parts)
Curve–surface integrals
In the following curve–surface integral theorems, S denotes a 2d open surface with a corresponding 1d boundary C = ∂S (a closed curve):
Integration around a closed curve in the clockwise sense is the negative of the same line integral in the counterclockwise sense (analogous to interchanging the limits in a definite integral): Bản mẫu:Block indent
Endpoint-curve integrals
In the following endpoint–curve integral theorems, P denotes a 1d open path with signed 0d boundary points and integration along P is from to :
Ma trận
Trong toán học, ma trận là một mảng chữ nhật– các số, ký hiệu, hoặc biểu thức, sắp xếp theo hàng và cột – mà mỗi ma trận tuân theo những quy tắc định trước. Từng ô trong ma trận được gọi là các phần tử hoặc mục. Ví dụ một ma trận có 2 hàng và 3 cột.
Kích thước hay cỡ của ma trận được định nghĩa bằng số lượng hàng và cột. Một ma trận m hàng và n cột được gọi là ma trận m × n hoặc ma trận m-nhân-n, trong khi m và n được gọi là chiều của nó. Ví dụ, ma trận A ở trên là ma trận 3 × 2.
Ma trận chỉ có một hàng gọi là vectơ hàng, ma trận chỉ có một cột gọi là vectơ cột. Ma trận có cùng số hàng và số cột được gọi là ma trận vuông. Ma trận có vô hạn số hàng hoặc số cột (hoặc cả hai) được gọi là ma trận vô hạn. Trong một số trường hợp, như chương trình đại số máy tính, sẽ có ích khi xét một ma trận mà không có hàng hoặc không có cột, goi là ma trận rỗng.
Tên gọi Độ lớn Ví dụ Miêu tả Vectơ hàng 1 × n Ma trận có một hàng, được dùng để biểu diễn một vectơ Vectơ cột n × 1 Ma trận có một cột, được dùng để biểu diễn một vectơ Ma trận vuông n × n Ma trận có cùng số hàng và số cột, nó được sử dụng để biểu diễn phép biến đổi tuyến tính từ một không gian vec tơ vào chính nó, như phép phản xạ, phép quay hoặc ánh xạ cắt.
Ký hiệu

Ma trận thường được viết trong dấu ngoặc vuông:
Một cách ký hiệu khác là sử dụng dấu ngoặc đơn lớn thay cho dấu ngoặc vuông:
Phép toán ma trận
Những tính chất tương tự đối với số thực có thể mở rộng ra đối với phép toán ma trận. Cộng hai ma trận có tính chất giao hoán, hay tổng của các ma trận không phụ thuộc vào thứ tự của phép tính:
- A + B = B + A.
- (A + B) + C = A + (B + C)
Phép chuyển vị có thể kết hợp với phép nhân vô hướng, cộng ma trận và nhân ma trận.
- (cA)T = c(AT)
- (A + B)T = AT + BT
- (AT)T = A
- (AB)T=BTAT
Phép toán Định nghĩa Ví dụ Cộng hai ma trận Tổng A+B của hai ma trận cùng kích thước m-x-n A và B được một ma trận cùng kích thước với phần tử trong vị trí tương ứng bằng tổng của hai phần tử tương ứng của mỗi ma trận: - (A + B)i,j = Ai,j + Bi,j, với 1 ≤ i ≤ m và 1 ≤ j ≤ n.
Nhân (vô hướng) một số với ma trận Tích cA của số c (cũng được gọi là vô hướng trong đại số trừu tượng) với ma trận A được thực hiện bằng cách nhân mỗi phần tử của A với c: - Bản mẫu:Nowrap begin(cA)i,j = c • Ai,j.Bản mẫu:Nowrap end
Phép toán này được gọi là nhân vô hướng, nhưng không nên nhầm lẫn với khái niệm "tích vô hướng" hay "tích trong".
Chuyển vị Chuyển vị của ma trận m-x-n A là ma trận n-x-m AT (cũng còn ký hiệu là Atr hay tA) tạo ra bằng cách chuyển hàng thành cột và cột thành hàng: - Bản mẫu:Nowrap begin(AT)i,j = Aj,i.Bản mẫu:Nowrap end
Tập hợp
Xắp sếp
Sếp đặt một số lượng vật vào vị trí nhứt định . Thí dụ như xắp sếp các ký tự từ a-z để tạo ra các chữ có 2 tự, 3 tự cho đến n tự . Xắp sếp các con số từ 0-9 để tạo ra các số có 1 con số , các số có 2 con số, các số có n con số
Thí dụ
Dùng các con số 0-9 để tạo ra
- Số có 1 con số , có 10 xắp sếp
- Số có 2 con số , có 10 x 9 = 90 xắp sếp
- Số có 3 con số , có 10 x 9 x 8 = 720 xắp sếp
Vậy,
Từ đó, ta có