Hàm số

Hàm số là một biểu thức đại số được dùng trong việc biểu diển tương quan giửa 2 đại lương với nhau . Thí dụ như

$y=2x+5$

Tính chất

Mọi hàm số đều có một hay nhiều hơn một biến số

Mọi hàm số của một biến số	$f(x)$	$y=2x$
Hàm số 2 biến số	$f(x,y)$	$r^2=x^2+y^2$ $f(r,\theta )$ . $Z\mathrm{\angle }\theta =\sqrt{(}{x}^2+y^2)\mathrm{\angle }ta{n}^{-1}\frac{y}{x}$
Hàm số 3 biến số	$f(x,y,z)$	$r^2=x^2+y^2+z^2$

Mọi hàm số đều có một giá trị

Hàm số bằng không	$f(x)=0$
Hàm số bằng hằng số không đổi	$f(x)=C$
Hàm số khác không	$f(x)=y(x)$

Loại hàm số

Dạng hàm số	Công thức	Thí dụ
Hàm số tuần hoàn (Periodic function)	$f(x)=f(x+T)$	$sinx=sin(x+k2\pi )$
Hàm số chẳn (Even function)	$f(x)=f(-x)$	$y(x)=|x|$
Hàm số lẽ (Odd function)	$f(x)=-f(x)$	$y(x)=-y(x)$
Hàm số nghịch đảo (Inverse function)	$f^{-1}(x)=\frac{1}{f(x)}$	$si{n}^{-1}x=\frac{1}{sinx}$
Hàm số trong hàm số (Composite function)	$f(x)=f(g(x))$
Hàm số nhiều biến số (Parametric function)	$z=f(x,y)$
Hàm số tương quan/]] (Recursive function)
Hàm số chia/]] (Rational function)	$Q(x)=\frac{N(x)}{M(x)}-R(x)$

Công thức toán của hàm số

Dạng hàm số	Công thức	Thí dụ
Hàm số đường thẳng	Hàm số đường thẳng qua 2 điểm bất kỳ $y=y_o+Z(x-x_o)$ Hàm số đường thẳng cắt trục tung ở điển b có độ dóc a $y=ax+b$
Hàm số vòng tròn	Hàm số vòng tròn Z đơn vị $Z^2=X^2+Y^2$
Hàm số vòng tròn 1 đơn vị	$(\frac{Z}{Z}{)}^2=(\frac{X}{Z}{)}^2+(\frac{Y}{Z}{)}^2$ $1=co{s}^2+si{n}^2$ $1=se{c}^2+ta{n}^2$ $1=cs{c}^2+co{t}^2$
Hàm số lũy thừa Power function	$y=a{x}^n$
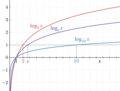
Hàm số Lô ga rít	$y(x)=Logx$
Hàm số lượng giác	$cos\theta =\frac{X}{Z}$ $sec\theta =\frac{1}{X}$ $csc\theta =\frac{1}{Y}$ $tan\theta =\frac{Y}{X}$ $cot\theta =\frac{X}{Y}$

Biểu diển Hàm số bằng tổng dải số lũy thừa

Maclaurin cho rằng mọi hàm số đều có thể biểu diển bằng tổng của dải số lũy thừa như sau

$f(x)=a_0+a_{1}x+a_2{x}^3+a_4{x}^4+...=f(0)+f^{\text{'}}x(0)+\frac{f^{{\text{'}}^{\prime }}(0)}{2!}+\frac{f^{{\text{'}}^{″}}(0)}{3!}+...$

Chứng minh

Khi x=0

$f(0)=a_0$

Khi lấy đạo hàm bậc nhứt của f(x) với giá trị x=0

$f^{\text{'}}(x)=a_1+2a_{2}x+3a_3{x}^2+4a_4{x}^3$

$f^{\text{'}}(0)=a_1$

Khi lấy đạo hàm bậc hai của f(x) với giá trị x=0

$f^{{\text{'}}^{\prime }}(x)=2a_2+(3)(2)a_{3}x+(4)(3)a_4{x}^2+(5)(4)a_5{x}^3$

$f^{{\text{'}}^{\prime }}(0)=2a_2$

$a_2=\frac{f^{{\text{'}}^{\prime }}(0)}{2}$

Khi lấy đạo hàm bậc ba của f(x) với giá trị x=0

$f^{{\text{'}}^{″}}(x)=(3)(2)a_{3}x+(4)(3)(2)a_{4}x+(5)(4)(3)a_5{x}^2$

$f^{{\text{'}}^{″}}(0)=(3)(2)a_3$

$a_3=\frac{f^{{\text{'}}^{″}}(0)}{3!}$

Thế $a_0,a-1,a-2$ vào hàm số ở trên $f(x)=a_0+a_{1}x+a_2{x}^3+a_4{x}^4$ ta được

$f(x)=f(0)+f^{\text{'}}x(0)+\frac{f^{{\text{'}}^{\prime }}(0)}{2!}+\frac{f^{{\text{'}}^{″}}(0)}{3!}$

Thí dụ

• $f(x)=\sin (x)$

$f(x)=\sin (x)$	$f(0)=\sin (0)=0$
$f^{{\text{'}}^{\prime }}(x)=-\sin (x)$	$f^{{\text{'}}^{\prime }}(0)=-\sin (0)=0$
$f^{{\text{'}}^{″}}(x)=-\cos (x)$	$f^{{\text{'}}^{″}}(0)=-\cos (0)=-1$
$f^{{\text{'}}^{‴}}(x)=\sin (x)$	$f^{{\text{'}}^{″}}(0)=\sin (0)=0$

$\sin (x)=0+x(1)+\frac{x^2}{2!}(0)+\frac{x^3}{3!}(-1)+\frac{x^5}{5!}(1)=x-\frac{x^3}{3!}+\frac{x^5}{5!}$

• $f(x)=\cos (x)$

$f(x)=\cos (x)$	$f(0)=\cos (0)=1$
$f^{\text{'}}(x)=-\sin (x)$	$f^{\text{'}}(0)=-\sin (0)=0$
$f^{{\text{'}}^{\prime }}(x)=-\cos (x)$	$f^{{\text{'}}^{″}}(0)=-\cos (0)=-1$
$f^{{\text{'}}^{‴}}(x)=\sin (x)$	$f^{{\text{'}}^{″}}(0)=\sin (0)=0$
$f^{{\text{'}}^{″}}(x)=\sin (x)$	$f^{{\text{'}}^{″}}(0)=\sin (0)=0$

$\cos (x)=1+x(0)+\frac{x^2}{2!}(-1)+\frac{x^3}{3!}(0)+\frac{x^4}{4!}(1)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}$

Đồ thị hàm số

Đồ Thị là một cách hiển thị Tọa độ của một điểm trên một mặt phẳng . Có hai loại đồ thị Đồ Thị điểm XY và Đồ Thị điểm Rθ

Đồ Thị điểm XY

Đồ thị	Hình	Ý nghỉa
Đồ Thị điểm XY		Đồ Thị XY là một Đồ Thị tạo bởi hai đường thẳng vuông góc với nhau . Một ngang, gọi là trục hoành hay trục x . Một dọc, gọi là trục tung hay trục y cắt nhau tại một điểm, gọi là điểm gốc có tọa độ (0,0) Một điểm, A , trên Đồ Thị XY sẽ có một tọa độ A(X,Y) với chiều dài X và độ cao Y . Thí dụ, Tọa độ của một điểm A(4,8) có x = 4 và y = 8 $X=Rcos\theta$ $Y=Rsin\theta$

Đồ Thị điểm Rθ

Đồ thị	Hình	Ý nghỉa
Đồ Thị điểm Rθ		Đồ Thị Vòng Tròn là một cách hiển thị Tọa độ của một điểm trên vòng tròn có Bán kín R ở Góc độ θ Khi một đường thẳng có độ dài R cắt đường chân trời (đường thẳng ngang) tại một điểm và tạo thành một góc θ. Trên mặt phẳng Rθ, đường bán kín R cắt đường chân trời tại một điểm gốc (R,0) . Trên mặt phẳng Rθ, Một điểm chuyển động theo vòng tròn sẻ có một tọa độ A(R,θ) và được biểu hiện như sau A = R/_θ $R^2=X^2+Y^2$ $Tan\theta =\frac{Y}{X}$

Đồ thị hàm số

Tương quan giửa 2 đại lượng x, y biểu thị bằng hàm sô

$y=x$

Lập bảng tương quan giửa hai giá trị x và y

x	-2	-1	0	1	2
y = x	-2	-1	0	1	2

Đặt điểm (x,y) trên đồ thi x-y ta có Đồ thị hàm số đường thẳng đi qua điểm gốc (0,0) có độ nghiêng bằng 1

Đồ thị của các hàm số cơ bản

Dạng hàm số	Công thức	Đồ thị
Hàm số đường thẳng	Hàm số đường thẳng qua 2 điểm bất kỳ $y=y_o+a(x-x_o)$ Hàm số đường thẳng cắt trục tung ở điển b có độ dóc a $y=ax+b$ . với $x_o=0,y_o=b$
Hàm số vòng tròn	Hàm số vòng tròn Z đơn vị $Z^2=X^2+Y^2$
Hàm số vòng tròn 1 đơn vị	${\frac{Z}{Z}}^2={\frac{X}{Z}}^2+{\frac{Y}{Z}}^2$ $1=co{s}^2+si{n}^2$ $1=se{c}^2+ta{n}^2$ $1=cs{c}^2+co{t}^2$
Hàm số lũy thừa Power function	$y=a{x}^n$
Hàm số Lô ga rít	$y(x)=Logx$
Hàm số lượng giác cos	$cos\theta =\frac{X}{Z}$
Hàm số lượng giác sin	$cos\theta =\frac{Y}{Z}$
Hàm số lượng giác sec	$cos\theta =\frac{1}{X}$
Hàm số lượng giác csc	$cos\theta =\frac{1}{Y}$
Hàm số lượng giác tan	$cos\theta =\frac{Y}{X}$
Hàm số lượng giác cot	$cos\theta =\frac{X}{Y}$

Line

Radial lines (those running through the pole) are represented by the equation $$\phi =\gamma ,$$ where $\gamma$ is the angle of elevation of the line; that is, $\phi =\arctan m$, where $m$ is the slope of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line $\phi =\gamma$ perpendicularly at the point $(r_0,\gamma )$ has the equation $$r(\phi )=r_0\sec (\phi -\gamma ).$$

Otherwise stated $(r_0,\gamma )$ is the point in which the tangent intersects the imaginary circle of radius $r_0$

Circle

A circle with equation Bản mẫu:Math

The general equation for a circle with a center at $(r_0,\gamma )$ and radius a is $$r^2-2r{r}_0\cos (\phi -\gamma )+r_0^2=a^2.$$

This can be simplified in various ways, to conform to more specific cases, such as the equation $$r(\phi )=a$$ for a circle with a center at the pole and radius a.

When Bản mẫu:Math or the origin lies on the circle, the equation becomes $$r=2a\cos (\phi -\gamma ).$$

In the general case, the equation can be solved for Bản mẫu:Math, giving $$r=r_0\cos (\phi -\gamma )+\sqrt{a^2-r_0^2{\sin }^2(\phi -\gamma )}$$ The solution with a minus sign in front of the square root gives the same curve.

Polar rose

A polar rose with equation Bản mẫu:Math

A polar rose is a mathematical curve that looks like a petaled flower, and that can be expressed as a simple polar equation, $$r(\phi )=a\cos (k\phi +{\gamma }_0)$$

for any constant γ₀ (including 0). If k is an integer, these equations will produce a k-petaled rose if k is odd, or a 2k-petaled rose if k is even. If k is rational, but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable a directly represents the length or amplitude of the petals of the rose, while k relates to their spatial frequency. The constant γ₀ can be regarded as a phase angle. Bản mẫu:Clear

Archimedean spiral

One arm of an Archimedean spiral with equation Bản mẫu:Math for Bản mẫu:Math

The Archimedean spiral is a spiral discovered by Archimedes which can also be expressed as a simple polar equation. It is represented by the equation $$r(\phi )=a+b\phi .$$ Changing the parameter a will turn the spiral, while b controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for Bản mẫu:Math and one for Bản mẫu:Math. The two arms are smoothly connected at the pole. If Bản mẫu:Math, taking the mirror image of one arm across the 90°/270° line will yield the other arm. This curve is notable as one of the first curves, after the conic sections, to be described in a mathematical treatise, and as a prime example of a curve best defined by a polar equation.

Ellipse, showing semi-latus rectum

Conic sections

A conic section with one focus on the pole and the other somewhere on the 0° ray (so that the conic's major axis lies along the polar axis) is given by: $$r=\frac{\ell }{1-e\cos \phi }$$ where e is the eccentricity and $\ell$ is the semi-latus rectum (the perpendicular distance at a focus from the major axis to the curve). If Bản mẫu:Nowrap, this equation defines a hyperbola; if Bản mẫu:Math, it defines a parabola; and if Bản mẫu:Math, it defines an ellipse. The special case Bản mẫu:Math of the latter results in a circle of the radius $\ell$. Bản mẫu:Clear

Intersection of two polar curves

The graphs of two polar functions $r=f(\theta )$ and $r=g(\theta )$ have possible intersections of three types:

1. In the origin, if the equations $f(\theta )=0$ and $g(\theta )=0$ have at least one solution each.
2. All the points $[g({\theta }_i),{\theta }_i]$ where ${\theta }_i$ are solutions to the equation $f(\theta +2k\pi )=g(\theta )$ where $k$ is an integer.
3. All the points $[g({\theta }_i),{\theta }_i]$ where ${\theta }_i$ are solutions to the equation $f(\theta +(2k+1)\pi )=-g(\theta )$ where $k$ is an integer.

Tóan hàm số

Thay đổi biến số

Thay đổi biến số x

$\mathrm{\Delta }x=(x+\mathrm{\Delta }x)-x$

Thay đổi biến số y

$\mathrm{\Delta }y=\mathrm{\Delta }f(x)=f(x+\mathrm{\Delta }x)-f(x)$

Biến đổi hàm số

Biến đổi hàm số tính bằng tỉ lệ thay đổi biến số y trên thay đổi biến số x

$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}=\frac{f(x+\mathrm{\Delta }x)-f(x)}{(x+\mathrm{\Delta }x)-x}$

Đạo hàm

Đạo hàm

v

$\frac{d}{dx}f(x)=f^{\text{'}}(x)=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum \frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum \frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$

Tích phân

Loại tích phân	Hình	Công thức
Tích phân xác định		$\underset{a}{\overset{b}{\int }}f(x)dx=F(b)-F(a)$
Tích phân bất định		$\int f(x)dx=\underset{\mathrm{\Delta }x\to 0}{\lim }\sum (f(x)+\frac{\mathrm{\Delta }f(x)}{2})\mathrm{\Delta }x=F(x)+C$